Автор идеи: Зуев Б.К.
Автор статьи: Выволокин В.В.
Введение
Атом водорода является простейшим по своей структуре. Как известно атом водорода имеет ядро, состоящее из одного протона, и одного электрона, расположенного на 1s-орбитали. Поскольку протон и электрон имеют разноименный заряд, то между ними действует сила Кулона. Также известно, что ядра атомов имеют собственный магнитный момент и следовательно собственное магнитное поле. При движение заряженных частиц в магнитном поле на них действует сила Лоренца, которая направлена перпендикулярно вектору скорости частицы и вектору магнитной индукции. Очевидно, что силы Кулона и силы Лоренца недостаточно, для того чтобы электрон оставался на своей орбитали, необходима также сила отталкивания между электроном и протоном. Современные квантовые представления не дают четкого ответа, чем конкретно вызвана квантованность орбиталей и следовательно энергий электрона в атоме. В рамках данной стать мы и рассмотрим причины квантования и получим уравнения описывающие поведения электрона в атоме. Напомню, что по современным представлениям положение электрона в атоме описывается вероятностным уравнение Шредингера. Мы же получим чисто механическое уравнение, которое даст возможность определить положение электрона в любой момент времени, что покажет несостоятельность принципа Гейзенберга.
Баланс сил
На рисунке 1 представлены все силы, которые действуют в атоме.
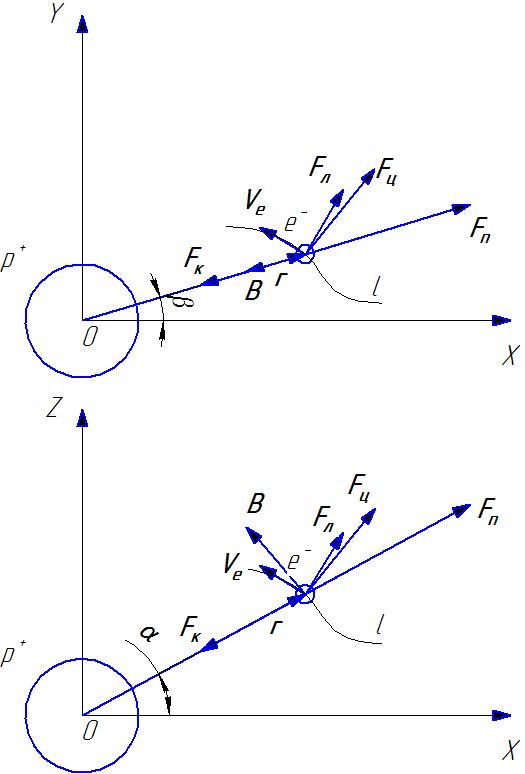
Запишем второй закон Ньютона для приведенной на рисунке системы сил.
![]() (1)
(1)
Запишем систему уравнений проекций этих сил на координатные оси XYZ.
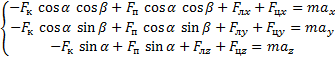 (2)
(2)
Здесь ![]() угол – это угол между радиус-вектором r(t) и плоскостью XY,
угол – это угол между радиус-вектором r(t) и плоскостью XY,
угол ![]() – угол между осью X и проекцией радиус-вектора r(t) на плоскость XY.
– угол между осью X и проекцией радиус-вектора r(t) на плоскость XY.
Распишем каждую силу в системе (2) через известные формулы с учетом их проекций на оси.
Сила Кулона
![]() , (3)
, (3)
где ![]() – электрическая постоянная равная
– электрическая постоянная равная ![]()
![]() – модуль заряда электрона или протона
– модуль заряда электрона или протона
![]() – координаты электрона в выбранной системе координат
– координаты электрона в выбранной системе координат
Потенциальная сила гравитационных волн
Подробнее об этой силе можно узнать из монографии [1]
![]() (4)
(4)
![]() – массы электрона и протона соответственно.
– массы электрона и протона соответственно.
X – Коэффициент пропорциональности численно равный квадрату скорости света.
Сила Лоренца
Как известно сила Лоренца вычисляется следующим образом
![]() (5)
(5)
Векторное произведение (5) может быть представлено в компонентах на оси ортогональной систему координат:
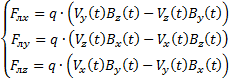 (6)
(6)
В системе уравнений (6) необходимо определить компоненты вектора магнитной индукции ![]() .
.
Поскольку магнитный момент ядра атома водорода вызван кольцевым током, движущихся в нем по-настоящему элементарных частиц [1], то в соответствии с законом Био-Савара-Лапласа, полученного для кольца с током, запишем компоненты вектора магнитной индукции:
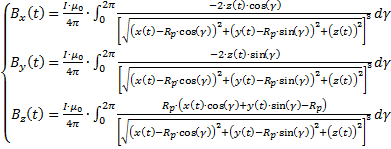 (7)
(7)
угол ![]() – это угол обхода кольцевого контура
– это угол обхода кольцевого контура
![]() – радиус протона
– радиус протона
![]() – сила тока в кольцевом контуре протона
– сила тока в кольцевом контуре протона
![]() – магнитная постоянная
– магнитная постоянная
Центробежная сила
Как известно центробежная сила действует по нормали к траектории движения тела и зависит от массы тела, кривизны траектории и скорости движения.
![]() (8)
(8)
![]() – мгновенная кривизна траектории
– мгновенная кривизна траектории
![]() – скорость электрона относительно начала координат
– скорость электрона относительно начала координат
![]() – вектор нормали к траектории движения электрона
– вектор нормали к траектории движения электрона
Мгновенная кривизна траектории определяется выражением
![]() (9)
(9)
![]() – первая и вторая производные от радиус-вектора
– первая и вторая производные от радиус-вектора ![]() по времени.
по времени.
Скорость электрона – есть корень из суммы квадратов его проекций на оси координат, которые в свою очередь являются первыми производными от проекций радиус-вектора по времени т.е.
![]() (10)
(10)
Единичный вектор нормали к траектории движения электрона ![]() определяется выражением
определяется выражением
![]() (11)
(11)
Раскрывая векторные произведения через компоненты вектора на оси координат, записывая радиус вектор через его компоненты, подставляем выражения (9), (10) и (11) в (8), получаем компоненты центробежной силы в проекциях на оси координат:
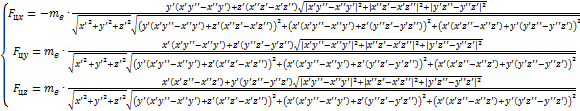 (12)
(12)
Определив проекции всех сил, входящих в систему уравнений (2) её можно переписать, учитывая следующие выражения:
![]()
![]()
![]()
![]()
Результирующая система имеет вид:
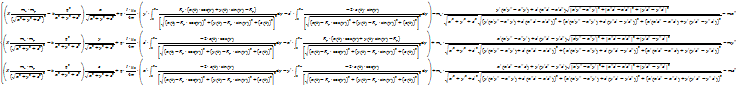
Найти аналитическое решение этой системы не представляется возможным. Решение можно получить численными методами решения систем дифференциальных уравнений второго порядка. Решение приведено в видео-ролике ниже.
Энергетические уровни электрона определяются целым количеством резонансных стоячих волн (шлейф пучностей за электроном), возникающих по траектории движения электрона. Если энергия поглощённого электроном фотона соответствует энергии необходимой для образования целого количества стоячих волн, движение электрона в них повторяется, делая их резонансными, тем самым фотон удерживается электроном определенное время и мы наблюдаем картину поглощения электроном фотона и затем его излучение. Фотоны, энергия которых не приводит к возникновению целого количества пучностей по траектории движения электрона, не захватываются, т.к. резонансной волны не образуется и картины поглощения-излучения не наблюдается.
Список использованных источников
1. Теория рождения и эволюции материи. Зуев Б.К. Самара: Изд-во “СамВен”, 1995.